This is the third page to my site about functions!

Sequences and Triangular Differences

  • In math, a sequence is an enumerated number of objects (most likely numbers) in which repetions are allowed
  • For example: Arithmetic sequence, Geometric sequence, Pascle's Triangle, Fibonacci's Sequence, etc..
  • For the many sequences shown, there is a generated equation for it: f(n)= an^k
  • n is an element of natural numbers (or counting numbers{1,2,3,...})
  • a is a real number
  • k is an element of the positive integers
  • You can derive this equation from a set of numbers, equating in the number of differences being the power of the x value
  • 1,4,9,16,25,36,49,64,81,... {original set of data}
  • 3,5,7,9,11,13,15,17,... {1st difference between the terms above}
  • 2,2,2,2,2,2,2,... {2nd difference between the terms above}
  • Once the numbers in the sequence of the difference become the same number, you have found the last difference
  • The final difference is the highest power of x in the equation, so because there were 2 differences, the equation is x²
  • The value of k is the number of differences that occur
  • The value of n can be found if you find the value that the numbers in the sequence are raised by {multiplied/addition/subtraction/division}
  • To find the value of a in the equation, you use the radical of k, multiplied by a, and set it equal to the constant {in this case 2}
  • When using triangular difference, you are trying to find the change in y, when you have the change in x

    • This is a simplified version:

    Function patterns

  • Sum-Sum {When both the x and y values are increasing via addition}
  • Sum-Constant Second Difference {When the y value is increasing via addition, but the x value has a common second difference}
  • Product-Product {When the x and y values are increasing via multiplication}
  • Sum-Product {When the x value is increasing via addition, but the y value is increasing via multiplication}
  • Product-Sum {When the y value is increasing via addition, but the x value is increasing via multiplication}
  • Sum-Sum {Linear}
  • Sum-Constant Second Difference {Quadratic}
  • Product-Product {Power}
  • Sum-Product {Exponential}
  • Product-Sum {Log}

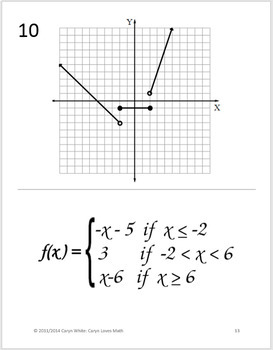
    • Piecewise functions

  • A Picewise function is a function that is sectioned into pieces
  • Different rules apply for a function, where the domain is in different "pieces"(or intervals)
  • It is formatted like so:
  • Some piecewise functions are not functions
  • If the function has two y values on one x value, one of those dots on the graph has to be open
  • If one of the values is not open, and there are two closed dots with different y values on an x value, then it is not a function

    • This is another example of a piecewise function:

    Quiz 3: put your knowledge of functions into use

    Question 1

    What are some examples of a sequence?

    domain, range, co-domain

    Arithmetic, Geometric, Pascal's Triangle

    Piecewise, Quadratic, Linear

    Question 2

    What do function patterns have to do with?

    The rate at which the range increases

    The rate at which the domain increases

    They have to deal with the domain and range of the function

    Question 3

    What pertains to a piecewise function?

    A piecewise function is a function where the function is sectioned into pieces

    A piecewise function has equations that are inverses of eachother equals x

    All of the above